Answer:
The maximum volume of the open box is 24.26 cm³
Explanation:
The volume of the box is given as
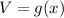 , where
, where
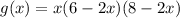 and
and
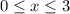 .
.
Expand the function to obtain:

Differentiate wrt x to obtain:
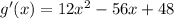
To find the point where the maximum value occurs, we solve
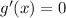
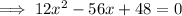
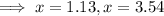
Discard x=3.54 because it is not within the given domain.
Apply the second derivative test to confirm the maximum critical point.
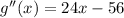 ,
,
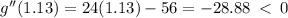
This means the maximum volume occurs at
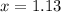 .
.
Substitute
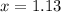 into
into
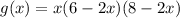 to get the maximum volume.
to get the maximum volume.
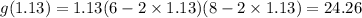
The maximum volume of the open box is 24.26 cm³
See attachment for graph.