Question

Consider the function V=g(x), where g(x) =x(6-2x)(8-2x), with x being the length of a cutout in cm and V being the volume of an open box in cm³, where x must between 0 and 3 cm. Determine the maximum volume of the open box in cm³. Round your answer to two decimal places. Also, indicate or show what process you used to obtain this answer. (Hint: graphing)

Answer 1

The maximum volume of the open box is 24.26 cm³

Explanation:

The volume of the box is given as
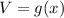`V=g(x)`, where
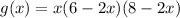`g(x)=x(6-2x)(8-2x)` and
`0\le x\le3`.

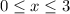Expand the function to obtain:

`g(x)=4x^3-28x^2+48x`

Differentiate wrt x to obtain:

`g'(x)=12x^2-56x+48`

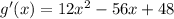
To find the point where the maximum value occurs, we solve

`g'(x)=0`

`\implies 12x^2-56x+48=0`

`\implies x=1.13,x=3.54`

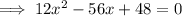
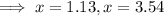
Discard x=3.54 because it is not within the given domain.

Apply the second derivative test to confirm the maximum critical point.

`g''(x)=24x-56`,
`g''(1.13)=24(1.13)-56=-28.88\:<\:0`

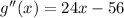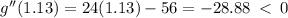
This means the maximum volume occurs at
`x=1.13`.

Substitute
`x=1.13` into
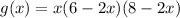`g(x)=x(6-2x)(8-2x)` to get the maximum volume.

`g(1.13)=1.13(6-2*1.13)(8-2*1.13)=24.26`

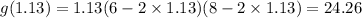
The maximum volume of the open box is 24.26 cm³

See attachment for graph.