Question

These tables represent an exponential function. Find the average rate of change for the interval from x=9 to x=10

Answer 1

B. 39,366

EXPLANATION

The y-values of the exponential function has the following pattern

`{3}^(0) = 1`

`{3}^(1) = 3`

`{3}^(2) = 9`

`{3}^(3) = 27`

:

:

`{3}^(x) = y`

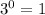
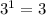
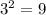
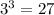
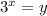
Or

`f(x) = {3}^(x)`

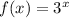
To find the average rate of change from x=9 to x=10, we simply find the slope of the secant line joining (9,f(9)) and (10,f(10))

This implies that,

`slope = (f(10) - f(9))/(10 - 9)`

`slope = \frac{ {3}^(10) - {3}^(9) }{1}`

`slope = (59049-19683)/(1) = 39366`

Therefore the average rate of change from x=9 to x=10 is 39366.

The correct answer is B.

Answer 2

Hi there!

The answer to this question is: B

Explanation:

The function for the question is: y=3^x

3^10=59049 and 3^9=19683

Then you just subtract the two numbers to get 39366