Question

A pendulum is made by letting a 2.0-kg object swing at the end of a string that has a length of 1.5 m. The maximum angle the string makes with the vertical as the pendulum swings is 30°. What is the speed of the object at the lowest point in its trajectory?

Answer 1

v = 1.978 m/s

Step-by-step explanation:

Given that,

Mass of the object, m = 2 kg

Length of the string, l = 1.5 m

The maximum angle the string makes with the vertical as the pendulum swings is 30°,
`\theta=30^(\circ)`

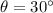
The pendulum have gravitational potential energy when the angle is maximum. The pendulum has only kinetic energy at its lowest point. Let v is the speed of the object at the lowest point in its trajectory. It can be calculated as :

`mgh=(1)/(2)mv^2`

h is the height moved by the pendulum.

`h=l(1-cos(30))`

`h=1.5(1-cos(30))`

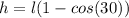
h = 0.2 m

`v=√(2gh)`

`v=√(2* 9.8* 0.2)`

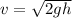
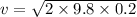
v = 1.978 m/s

So, the speed of the object at the lowest point in its trajectory is 1.978 m/s.

Answer 2

v = 2 m/s

Step-by-step explanation:

Here we can use energy conservation to find the speed at the lowest point on its trajectory

As we know that by energy conservation

initial total gravitational potential energy = final total kinetic energy

now the height that is moved by the pendulum while it swing down is given as

`h = L(1 - cos30)`

`h = 1.5(1 - cos30) = 0.200 m`

now we can use energy conservation as

`mgh = (1)/(2)mv^2`

`v = √(2gh)`

`v = √(2(9.8)(0.200))`

`v = 2 m/s`