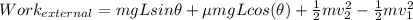Answer:
Work done by external force is given as
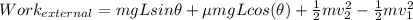
Step-by-step explanation:
As per work energy Theorem we can say that work done by all force on the car is equal to change in kinetic energy of the car
so we will have
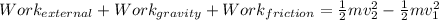
now we have

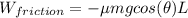
so from above equation
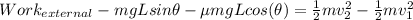
so from above equation work done by external force is given as