Question

The center of a circle is located at (6, −1) . The radius of the circle is 4.

What is the equation of the circle in general form?


x2+y2−12x+2y+21=0

x2+y2−12x+2y+33=0

x2+y2+12x−2y+21=0

x2+y2+12x−2y+33=0

Answer 1

`\bf \textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \qquad center~~(\stackrel{6}{ h},\stackrel{-1}{ k})\qquad \qquad radius=\stackrel{4}{ r} \\\\[-0.35em] ~\dotfill\\[1em] [x-6]^2+[y-(-1)]^2=4^2\implies (x-6)^2+(y+1)^2=16 \\\\\\ \stackrel{\mathbb{F~O~I~L}}{(x^2-12x+36)}+\stackrel{\mathbb{F~O~I~L}}{(y^2+2y+1)}=16\implies x^2+y^2-12x+2y+37=16 \\\\\\ x^2+y^2-12x+2y+37-16=0\implies x^2+y^2-12x+2y+21=0`

Answer 2

Option A

Step-by-step explanation

When a circle has it's center at (h,k) and and radius r units, then its equation in standard form is

`{(x - h)}^(2) + {(y - k)}^(2) = {r}^(2)`

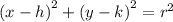
The given circle has its center at (6,-1) and its radius is r=4 units.

We plug in these values to get

`{(x - 6)}^(2) + {(y - - 1)}^(2) = {4}^(2)`

`{(x - 6)}^(2) + {(y + 1)}^(2) =16`

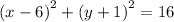
We now expand to obtain

`{x}^(2) - 12x + 36 + {y}^(2) + 2y + 1 = 16`

`{x}^(2) + {y}^(2) - 12x +2 y + 36 + 1 - 16 = 0`

`{x}^(2) + {y}^(2) - 12x +2 y + 21 = 0`

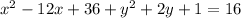
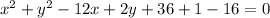
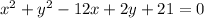
This is the equation in general form of the circle.