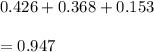Question

roduction records indicate that 2.8​% of the light bulbs produced in a facility are defective. A random sample of 30 light bulbs was selected. a. Use the binomial distribution to determine the probability that fewer than three defective bulbs are found.

Answer 1

Answer: Our required probability is 0.947.

Explanation:

Since we have given that

Number of light bulbs selected = 30

Probability that the light bulb produced in a facility are defective = 2.8% = 0.028

We need to find the probability that fewer than 3 defective bulbs are found.

We will use "Binomial distribution":

n = 30, p = 0.028

so, P(X>3)=P(X=0)+P(X=1)+P(X=2)

So, it becomes,

`P(X=0)=(1-0.0.28)^(30)=0.426`

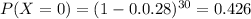
and

`P(X=1)=^(30)C_1(0.028)(0.972)^(29)=0.368\\\\P(X=2)=^(30)C_2(0.028)^2(0.972)^28=0.153`

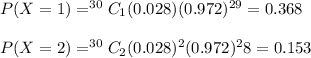
So, the probability that fewer than three defective bulbs are defective is given by

`0.426+0.368+0.153\\\\=0.947`