Answer:
The difference in the length of the two rods when compressed is
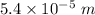 .
.
Step-by-step explanation:
Given that,
Length = 0.780 m
Diameter = 1.50 cm
Force = 4350 N
(a). For steel rod
We know ,
The young modulus for steel rod
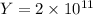
Using formula of young modulus
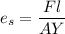
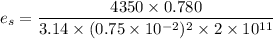
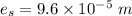
(b). For copper rod
We know ,
The young modulus for steel rod
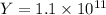
Using formula of young modulus
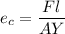
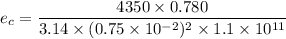
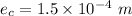
The difference in the length of the two rods when compressed is
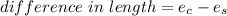
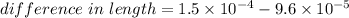
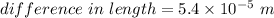
Hence, The difference in the length of the two rods when compressed is
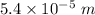 .
.