Answer: 0.3679
Explanation:
The formula for Poisson distribution :-
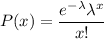
Let x be the number of breakdowns.
Given : The rate of breakdown per week : 0.5
Then , for 2 weeks period the number of breakdowns =
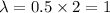
Then , the probability that there will be no breakdown on his car in the trip is given by :-
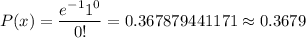
Hence, the required probability : 0.3679