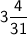Answer:
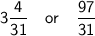
-------------------------------------------------------------------------------------------------------
The given expression:
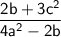
Here given a = 8, b = 4, and c = 16
Inserting this values
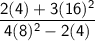
Simplify following
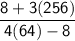
Distribute inside parenthesis
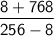
Add/Subtract similar terms
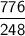
Simplify following, in improper fraction
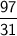
In mixed fraction, answer: