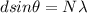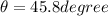Answer:
Part a)
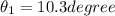
Part b)
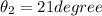
Part c)

Part d)
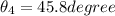
Step-by-step explanation:
For the position of dark fringe the path difference of light is odd multiple of half of the wavelength
so here we will have
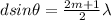
part a)
for m = 0 we have
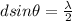

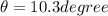
Part b)
Similarly for the maximum intensity we will have path difference must be integral multiple of wavelength
so we have
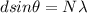
for m = 1 we have

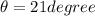
Part c)
for m = 1 we have
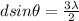
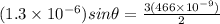

Part d)
for m = 2 again we have