Answer:
1. The values of |PQ|, |QR| and |RP| are 3, 3√5 and 6 respectively.
2. No.
3. No.
Explanation:
The vertices of given triangle are P(0, 1, 5), Q(2, 3, 4), R(2, −3, 1).
Distance formula:
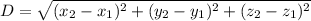
Using distance formula we get
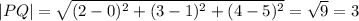
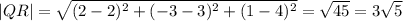
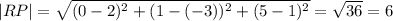
The values of |PQ|, |QR| and |RP| are 3, 3√5 and 6 respectively.
In a right angled triangle the sum of squares of two small sides is equal to the square of third side.
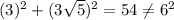
Therefore PQR is not a right angled triangle.
In an isosceles triangle, the length of two sides are equal.
The measure of all sides are different, therefore PQR is not an isosceles triangle.