Answer:
The 95% confidence interval for the true mean speed of thunderstorms is [10.712, 13.688].
Explanation:
Given information:
Sample size = 10
Sample mean = 12.2 mph
Standard deviation = 2.4
Confidence interval = 95%
At confidence interval 95% then z-score is 1.96.
The 95% confidence interval for the true mean speed of thunderstorms is
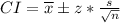
Where,
 is sample mean, z* is z score at 95% confidence interval, s is standard deviation of sample and n is sample size.
is sample mean, z* is z score at 95% confidence interval, s is standard deviation of sample and n is sample size.
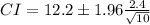
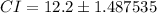
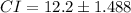
![CI=[12.2-1.488, 12.2+1.488]](https://img.qammunity.org/2020/formulas/mathematics/college/ycdjdg4wei7npw1wxpy1lk1i9h9p83ulfy.png)
![CI=[10.712, 13.688]](https://img.qammunity.org/2020/formulas/mathematics/college/dr749z5tmcjs3ohb3k82xn3b8mov17eknu.png)
Therefore the 95% confidence interval for the true mean speed of thunderstorms is [10.712, 13.688].