Question

Suppose you just received a shipment of thirteen televisions. Three of the televisions are defective. If two televisions are randomly​ selected, compute the probability that both televisions work. What is the probability at least one of the two televisions does not​ work?

Answer 1

Answer: 0.4083

Explanation:

Let D be the event of receiving a defective television.

Given : The probability that the television is defective :-

`P(D)=(3)/(13)`

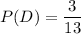
The formula for binomial distribution :-

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

If two televisions are randomly​ selected, compute the probability that both televisions work, then the probability at least one of the two televisions does not​ work is given by :_

`P(X\geq1)=P(1)+P(2)\\\\=^2C_1((3)/(13))^1(1-(3)/(13))^(2-1)+^2C_2((3)/(13))^2(1-(3)/(13))^(2-2)\\\\=0.408284023669\approx0.4083`

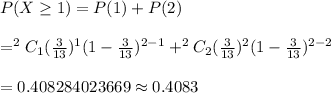
Hence , the required probability = 0.4083