Question

For the month of January in a certain​ city, 42​% of the days are cloudy. Also in the month of January in the same​ city, 41​% of the days are cloudy and rainy. What is the probability that a randomly selected day in January will be rainy if it is cloudy​?

Answer 1

Answer: 0.9762

Explanation:

Let A be the event that days are cloudy and B be the event that days are rainy for January month .

Given : The probability that the days are cloudy =
`P(A)=0.42`

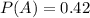
The probability that the days are cloudy and rainy =
`P(A\cap B)=0.41`

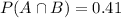
Now, the conditional probability that a randomly selected day in January will be rainy if it is cloudy is given by :-

`P(B|A)=(P(B\cap A))/(P(A))\\\\\Rightarrow\ P(B|A)=(0.41)/(0.42)=0.97619047619\approx0.9762`

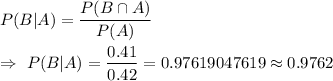
Hence, the probability that a randomly selected day in January will be rainy if it is cloudy = 0.9762