Question

A billiard ball moving at 6.00 m/s strikes a stationary ball of the same mass. After the collision, the first ball moves at 5.21 m/s at an angle of 29.7° with respect to the original line of motion. Assuming an elastic collision (and ignoring friction and rotational motion), find the struck ball's velocity after the collision.

Answer 1

Velocity is 3.11 m/s at an angle of -56° with respect to the original line of motion.

Step-by-step explanation:

Let line of action be horizontal axis , mass of ball be m and unknown velocity be v.

Here momentum is conserved.

Initial momentum =Final momentum

Initial momentum = m x 6i + m x 0i = 6m i

Final momentum = m x (5.21cos 29.7 i + 5.21sin 29.7 j) + m x v = 4.26 m i + 2.58 m j + m v

4.26 m i + 2.58 m j + m v = 6m i

v = 1.74 i - 2.58 j

Magnitude of velocity
`=√(1.74^2+(-2.58)^2)=3.11m/s`

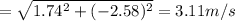
Direction,

`\theta =tan^(-1)\left ( (-2.58)/(1.74)\right )=--56^0`

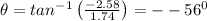
Velocity is 3.11 m/s at an angle of -56° with respect to the original line of motion.