Answer:
The formula to solve r is
![r=\sqrt[3]{(GMT^(2))/(4\pi^(2))}](https://img.qammunity.org/2020/formulas/mathematics/high-school/26zlglht5pdhc2iqnl7xka55y8l6s2ycaq.png) .
.
Explanation:
Consider the provided formula:

Where r is the orbit’s mean radius, M is the mass of the planet, and G is the universal gravitational constant.
Multiply both side by GM.

Further solve the above equation.
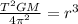
![\sqrt[3]{(GMT^(2))/(4\pi^(2))}=r](https://img.qammunity.org/2020/formulas/mathematics/high-school/2lp77b2u4395mliddby1fankzrl66fi3m0.png)
Hence, the formula to solve r is
![r=\sqrt[3]{(GMT^(2))/(4\pi^(2))}](https://img.qammunity.org/2020/formulas/mathematics/high-school/26zlglht5pdhc2iqnl7xka55y8l6s2ycaq.png) .
.