Answer:
Explanation:
There are 3 ways to find the other x intercept.
1) Polynomial Long Division.
Divide x^2 - 3x + 2 by the binomial x - 2, because by the Factor Theorem if a is a root of a polynomial then x - a is a factor of said polynomial.
2) Just solving for x when y = 0, by using the quadratic formula.
 .
.
So the other x - intercept is at (1, 0)
3) Using Vietta's Theorem regarding the solutions of a quadratic
Namely, the sum of the solutions of a quadratic equation is equal to the quotient between the negative coefficient of the linear term divided by the coefficient of the quadratic term.

And the product between the solutions of a quadratic equation is just the quotient between the constant term and the coefficient of the quadratic term.
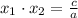
These relations between the solutions give us a brief idea of what the solutions should be like.