Question

A proton travels at a speed 0.25 x 10^7 m/s perpendicular to a magnetic field. The field causes the proton to travel in a circular path of radius 0.975 m. What is the field strength, in tesla?

Answer 1

The magnetic field strength of the proton is 0.026 Tesla.

Step-by-step explanation:

It is given that,

Speed of the proton,
`v=0.25* 10^7\ m/s`

The radius of circular path, r = 0.975 m

It is moving perpendicular to a magnetic field such that the magnetic force is balancing the centripetal force.

`qvB\ sin90=(mv^2)/(r)`

`B=(mv)/(qr)`

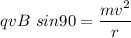
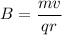
q = charge on proton

`B=(1.67* 10^(-27)\ kg* 0.25* 10^7\ m/s)/(1.6* 10^(-19)\ C* 0.975\ m)`

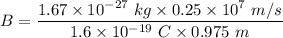
B = 0.026 Tesla

So, the magnetic field strength of the proton is 0.026 Tesla.