Answer:
the solution is x = 0
Explanation:
We know the fact that if the column of the square matrix is linearly independent then the determinant of the matrix is non zero.
Now, since the determinant of the matrix is not zero then the inverse of the matrix must exists.
Therefore, we have

Now, for the equation Ax =0
multiplying both sides by
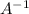

From equation (i)
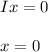
Therefore, the solution is x = 0