Answer:
The weight of the astronaut is 0.4802 N.
Step-by-step explanation:
Gravitational potential energy,
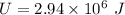
Distance above earth,
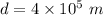
The gravitational potential energy is given by :
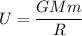
G is universal gravitational constant
M is the mass of Earth,
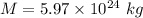
m is mass of astronaut
R is the radius of earth, R = R + d
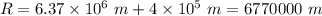
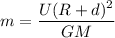
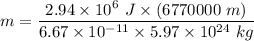
m = 0.049 kg
The weight of the astronaut is given by :
W = mg
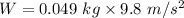
W = 0.4802 N
So, the weight of the astronaut when he returns to the earth surface is 0.4802 N. Hence, this is the required solution.