Question

A circle has a radius of 5 ft, and an arc of length 7 ft is made by the intersection of the circle with a central angle. Which

equation gives the measure of the central angle, q?

Answer 1

To work out the central angle, you just re-arrange the equation for the length of an arc:

Equation for length of an arc:

`(angle)/(360)` ×
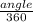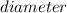`diameter` × π =
`length of arc`

We can arrange this to work out the central angle, q. But first, lets substitute in all of the values that we know:

angle = q

diameter = 5 x 2 = 10 ft

length of arc = 7

[Substitute in]

`(q)/(360)` ×
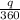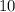`10`π =
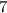`7` (Now just rearrange for q)

`(q)/(360)` =
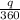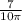`(7)/(10\pi )` (multiply both sides by 360 to get q)

`q` =
`(7)/(10\pi )` ×
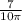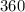`360` (now just simplify)

`q` =
`(252)/(\pi )`

=
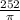
`80.214` (rounded to 3 decimal places)

______________________________

Therefore:

The equation that gives you ange q is:

`q` =
`(length.of.arc)/(diamater.times.\pi )` ×
`360`

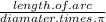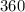
and q = 80.214 when all of the values are substituted in.

Answer 2

B q=7/5

Explanation:

Well Q=s/r and they said a Radius of 5 Which puts 5 at the bottom.

Then an arc length of 7 Which =S. so q=7/5