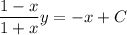Divide both sides by
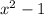 to get a linear ODE,
to get a linear ODE,
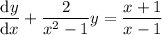
In order for this operation to be valid in the first place, we require that
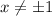 (since that would make
(since that would make
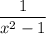 undefined, which we don't want to happen). Then we are forcing any solution to the ODE to exist on any of the three intervals,
undefined, which we don't want to happen). Then we are forcing any solution to the ODE to exist on any of the three intervals,
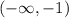 ,
,
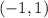 , or
, or
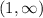 , and either the first or third of these can be chosen as the largest interval.
, and either the first or third of these can be chosen as the largest interval.
In case you also need to solve the ODE: Multiply both sides by
 , so that
, so that

Then the left side can be condensed as the derivative of a product, since
![(\mathrm d)/(\mathrm dx)\left[(1-x)/(1+x)\right]=-\frac2{(1+x)^2}](https://img.qammunity.org/2020/formulas/mathematics/college/lywxy1ixofwqdqirhwl6v7xyjmzungwuoy.png)
and we have
![(\mathrm d)/(\mathrm dx)\left[(1-x)/(1+x)y\right]=-1](https://img.qammunity.org/2020/formulas/mathematics/college/tpq7vfxn4089k9sls6bh28bqp3s1mzjlby.png)
Integrate both sides:
![\displaystyle\int(\mathrm d)/(\mathrm dx)\left[(1-x)/(1+x)y\right]\,\mathrm dx=-\int\mathrm dx](https://img.qammunity.org/2020/formulas/mathematics/college/yg4limmkf2xb4d493dg21mr2v69mn1cbbm.png)