Question

1. Provide an appropriate response.

A company estimates that it will sell N(t) hair dryers after spending $t thousands on advertising as given by:
N(t) = -3t3 + 450t2 - 21,600t + 1,100, 40 ? t ? 60 For which values of t is the rate of sales N'(t) increasing?

A. 50 < t < 60 B. 40 < t < 50. C. t > 40 D. 40< t < 60

Answer 1

D. 40 < t < 60

Explanation:

Given function,

`N(t) = -3t^3 + 450t^2 - 21,600t + 1,100`

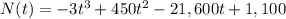
Differentiating with respect to x,

`N(t) = -9t^2+ 900t - 21,600`

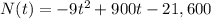
For increasing or decreasing,

f'(x) = 0,

`-9t^2+ 900t - 21,600=0`

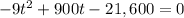
By the quadratic formula,

`t=(-900\pm √(900^2-4* -9* -21600))/(-18)`

`t=(-900\pm √(32400))/(-18)`

`t=(-900\pm 180)/(-18)`

`\implies t=(-900+180)/(-18)\text{ or }t=(-900-180)/(-18)`

`\implies t=40\text{ or }t=60`

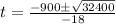
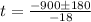
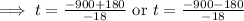
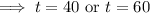
Since, in the interval -∞ < t < 40, f'(x) = negative,

In the interval 40 < t < 60, f'(t) = Positive,

While in the interval 60 < t < ∞, f'(t) = negative,

Hence, the values of t for which N'(t) increasing are,

40 < t < 60,

Option 'D' is correct.