Question

The volume of a rectangular prism is (x^4+4x^3+3x^2+8x+4), and the area of its base is (x^3+ 3x^2+8). If the volume of a rectangular prism is the product of its base area and height, what is the height of the prism

Answer 1

Explanation:

Answer 2

height of prism =
`x+1-(4)/(x^3+3x^2+8)`

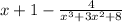
Explanation:

Volume of rectangular prism = (x^4+4x^3+3x^2+8x+4)

Area of its bases = (x^3+ 3x^2+8)

Height of prism = ?

Volume of rectangular Prism = Area of its bases * Height of prism

(x^4+4x^3+3x^2+8x+4) = (x^3+ 3x^2+8) * height of prism

=> height of prism = (x^4+4x^3+3x^2+8x+4) /(x^3+ 3x^2+8)

=> height of prism =
`x+1-(4)/(x^3+3x^2+8)`

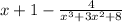
The division of (x^4+4x^3+3x^2+8x+4) /(x^3+ 3x^2+8) is shown in the attached figure.