Question

The value of Jennifer's stock portfolio (in dollars) is given by the function f(t) = -3t +72t + 5000, where t is the time in months since she opened the account. After how many months will her portfolio be at a maximum? What is the maximum value of the portfolio?

Answer 1

a) The portfolio will be at maximum after 12 months (1 year)

b) The maximum value of the portfolio is $5432

Explanation:

The function that models Jennifer's stock portfolio (in dollars) is
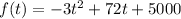`f(t)=-3t^2+72t+5000`, where t is the time in months since she opened the account.

We complete the square to obtain this function in vertex form:

Factor -3 from the first two terms

`f(t)=-3(t^2-24t)+5000`.

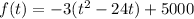Add the zero pairs -3(+144),-3(-144)

`f(t)=-3(t^2-24t+144)+5000+-3(-144)`.

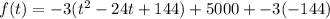Factor the perfect square trinomial and simplify.

`f(t)=-3(t-12)^2+5432`.

The vertex of this function is (h,k)=(12,5432)

a) The portfolio will be at maximum when t=12, the h-value of the vertex

b) The maximum value of the portfolio is the k-value of the vertex which is 5432