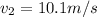Answer:
v = 10.1 m/s
Step-by-step explanation:
As we know that by the law of conservation of volume the rate of volume flowing through the pipe will remain conserved
so here we have flow rate given as

now we have
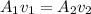
now we have



now from above equation we have