Answer:
Option C and D
Explanation:
To find : After being rearranged and simplified, which of the following equations could be solved using the quadratic formula? Check all that apply.
Solution :
Quadratic equation is
 with solution
with solution
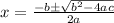
A.
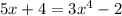
Simplifying the equation,
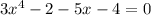
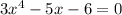
It is not a quadratic equation.
B.
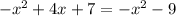
Simplifying the equation,


It is not a quadratic equation.
C.
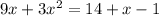
Simplifying the equation,
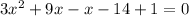
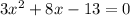
It is a quadratic equation where a=3, b=8 and c=-13.
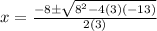
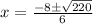
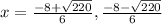
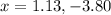
D.
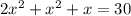
Simplifying the equation,
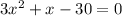
It is a quadratic equation where a=3, b=1 and c=-30.
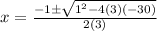
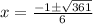
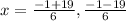
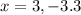
Therefore, option C and D are correct.