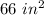For this case we have that the area of the figure is given by the sum of the area of a rectangle plus the area of a triangle.
By definition, the area of a reactangle is given by:
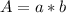
Where:
a, b:they are the sides of the rectangle.
According to the figure we have:
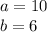
Substituting we have:
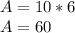
Thus, the area of the rectangle is
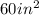
On the other hand, the area of a triangle is given by:
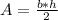
Where:
b is the base and h is the height of the triangle.
According to the figure we have to:
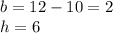
Substituting in the formula:
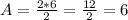
Thus, the area of the rectangle is
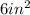
Then, the total area of the figure is:
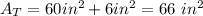
Answer: