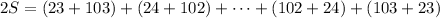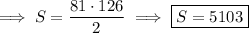Question

Find the sum of 23+24+25+...+103

Answer 1

Let

`S=23+24+25+\cdots+101+102+103`

This sum has ___ terms. Its terms form an arithmetic progression starting at 23 with common difference between terms of 1, so that the
`n`-th term is given by the sequence
`23+(n-1)\cdot1=22+n`. The last term is 103, so there are

`103=22+n\implies n=81`

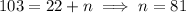
terms in the sequence.

Now, we also have

`S=103+102+101+\cdots+25+24+23`

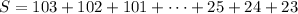
so that adding these two ordered sums together gives

`2S=(23+103)+(24+102)+\cdots+(102+24)+(103+23)`

`\implies2S=\underbrace{126+126+\cdots+126+126}_{81\text{ times}}=81\cdot126`

`\implies S=\frac{81\cdot126}2\implies\boxed{S=5103}`