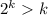Question

Use induction to prove that 2? ?? for any integer n>0 . Indicate type of induction used.

I proved the base case using n = 1, and for my induction hypothesis, I said that we assume n = k for 2^k > k, but I am stuck trying to get to n = k + 1.

So far I have:

2^k > k

2*2^k > 2*k

2^{k+1} > 2k

Answer 1

Answer with explanation:

The given statement is which we have to prove by the principal of Mathematical Induction

`2^(n)>n`

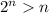
1.→For, n=1

L H S =2

R H S=1

2>1

L H S> R H S

So,the Statement is true for , n=1.

2.⇒Let the statement is true for, n=k.

`2^(k)>k`

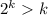
---------------------------------------(1)

3⇒Now, we will prove that the mathematical statement is true for, n=k+1.

`\rightarrow 2^(k+1)>k+1\\\\L H S=\rightarrow 2^(k+1)=2^(k)* 2\\\\\text{Using 1}\\\\2^(k)>k\\\\\text{Multiplying both sides by 2}\\\\2^(k+1)>2k\\\\As, 2 k=k+k,\text{Which will be always greater than }k+1.\\\\\rightarrow 2 k>k+1\\\\\rightarrow2^(k+1)>k+1`

Hence it is true for, n=k+1.

So,we have proved the statement with the help of mathematical Induction, which is

`2^(k)>k`