Answer: 0.1052
Explanation:
Given : Mean :
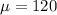
Standard deviation :
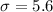
We assume the variable is normally distributed.
The formula for z-score is given by :-
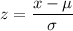
For x=120.4
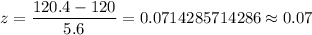
For x=121.9
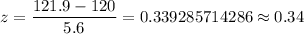
The p-value =
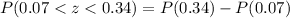
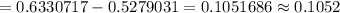
The probability that the individual's pressure will be between 120.4 and 121.9 mm Hg = 0.1052