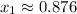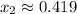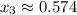Question

Solve the system of equation by guess sidle method

8x1 + x2 + x3 = 8

2x1 + 4x2 + x3 = 4

x1 + 3x2 + 5x3 = 5

Answer 1

Answer: The solution is,

`x_1\approx 0.876`

`x_2\approx 0.419`

`x_3\approx 0.574`

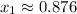
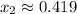
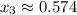
Explanation:

Given equations are,

`8x_1 + x_2 + x_3 = 8`

`2x_1 + 4x_2 + x_3 = 4`

`x_1 + 3x_2 + 5x_3 = 5`,

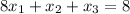
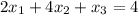
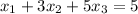From the above equations,

`x_1=(1)/(8)(8-x_2-x_3)`

`x_2=(1)/(4)(4-2x_1-x_3)`

`x_3=(1)/(5)(5-x_1-3x_2)`

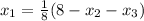
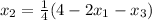
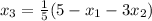
First approximation,

`x_1(1)=(1)/(8)(8-(0)-(0))=1`

`x_2(1)=(1)/(4)(4-2(1)-(0))=0.5`

`x_3(1)=(1)/(5)(5-1-3(0.5))=0.5`

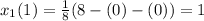
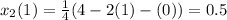
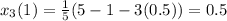
Second approximation,

`x_1(2)=(1)/(8)(8-(0.5)-(0.5))=0.875`

`x_2(2)=(1)/(4)(4-2(0.875)-(0.5))=0.4375`

`x_3(2)=(1)/(5)((0.875)-3(0.4375))=0.5625`

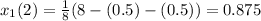
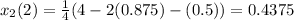
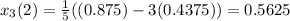
Third approximation,

`x_1(3)=(1)/(8)(8-(0.4375)-(0.5625))=0.875`

`x_2(3)=(1)/(4)(4-2(0.875)-(0.5625))=0.421875`

`x_3(3)=(1)/(5)(5-(0.875)-3(0.421875))=0.571875`

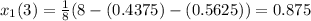
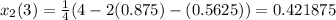
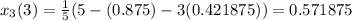
Fourth approximation,

`x_1(4)=(1)/(8)(8-(0.421875)-(0.571875))=0.875781`

`x_2(4)=(1)/(4)(4-2(0.875781)-(0.571875))=0.419141`

`x_3(4)=(1)/(5)(5-(0.875781)-3(0.419141))=0.573359`

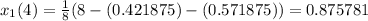
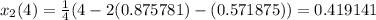
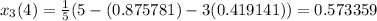
Fifth approximation,

`x_1(5)=(1)/(8)(8-(0.419141)-(0.573359))=0.875938`

`x_2(5)=(1)/(4)(4-2(0.875938)-(0.573359))=0.418691`

`x_3(5)=(1)/(5)(5-(0.875938)-3(0.418691))=0.573598`

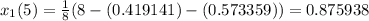
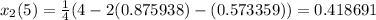
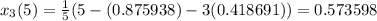
Hence, by the Gauss Seidel method the solution of the given system is,

`x_1\approx 0.876`

`x_2\approx 0.419`

`x_3\approx 0.574`