Question

Due in 1 hours, 24 minutes. Due Fri 06/28/2019 11:59 p A survey team is trying to estimate the height of a mountain above a level plain. From one point on the plain, they observe that the angle of elevation to the top of the mountain is 24°. From a point 1000 feet closer to the mountain along the plain, they find that the angle of elevation is 26 How high (in feet) is the mountain? Preview

Answer 1

Height of the mountain is 5108.80 feet.

Explanation:

From the figure attached, h is the height of a mountain AB.

At a point C angle of elevation of the mountain is 24°

Now survey team gets closer to the mountain by 1000 feet then angle of elevation is 26°.

Now from ΔABC,

tan24 =
`(h)/(x+1000)`

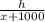
0.445 =
`(h)/(x+1000)`

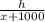
h = 0.445(x + 1000)------(1)

From ΔABD,

tan26 =
`(h)/(x)`

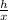
0.4877 =
`(h)/(x)`

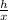
h = 0.4877x -----(2)

Now we equation 1 and equation 2

0.4452(x + 1000) = 0.4877x

0.4877x - 0.4452x = 1000(0.4452)

0.0425x = 445.20

x =
`(445.20)/(0.0425)`

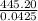
x = 10475.29 feet

Now we plug in the value of x in equation 2.

h = (10475.29)×(0.4877)

h = 5108.80 feet

Therefore, height of the mountain is 5108.80 feet