Answer:
The height of tower is 322.7 feet.
Explanation:
Given
Distance between a building and tower= 250 feet
BCDE is a rectangle .Therefore, we have BC=ED and CD=BE=250 feet
In triangle ABE
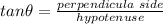
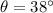
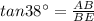
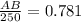
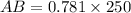
AB=195.25 feet
In triangle EDC
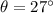
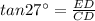
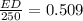
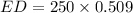
ED=127.25 feet
ED=BC=127.25 feet
The height of tower=AB+BC
The height of tower=195.25+127.25=322.5 feet