Answer:
15 subsets of cardinality 4 contain at least one odd number.
Explanation:
Here the given set,
S={1,2,3,4,5,6},
Since, a set having cardinality 4 having 4 elements,
The number of odd digits = 3 ( 1, 3, 5 )
And, the number of even digits = 3 ( 2, 4, 6 )
Thus, the total possible arrangement of a set having 4 elements out of which atleast one odd number =
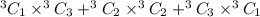
By using
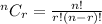 ,
,
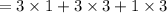
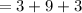
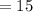
Hence, 15 subsets of cardinality 4 contain at least one odd number.