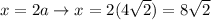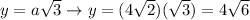Question

2 Geometry Questions thank you guys :):)

Answer 1

6.
`\displaystyle 4√(6) = y \\ 4√(2) = x`

5.
`\displaystyle 45√(2) = x`

Step-by-step explanation:

30°-60°-90° Triangles

Hypotenuse → 2x

Short Leg → x

Long Leg → x√3

45°-45°-90° Triangles

Hypotenuse → x√2

Two identical legs → x

6. You solve the shorter triangle first:

`\displaystyle a^2 + b^2 = c^2 \\ \\ \\ x^2 + x^2 = 8^2 \\ \\ (2x^2)/(2) = (64)/(2) → √(x^2) = √(32) \\ \\ 4√(2) = x`

Now that we know our x-value, we can solve the larger triangle:

`\displaystyle 4√(6) = 4√(2)√(3) \\ \\ 4√(6) = y`

5. This exercise is EXTREMELY SIMPLE since two congruent isosceles right triangles form that square, so all you have to do, according to the rules for 45°-45°-90° triangles, is attach
`\displaystyle √(2)`to 45, giving you
`\displaystyle 45√(2).`

I am joyous to assist you anytime.

Answer 2

`\large\boxed{Q5.\ x=45\sqrt2}\\\boxed{Q6.\ x=8\sqrt2,\ y=4\sqrt6}`

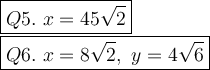
Explanation:

Q5.

x it's a diagonal of a square.

The formula of a length of diagonal of a square:

`d=a\sqrt2`

a - side of a square

We have a = 45.

Substitute:

`x=45\sqrt2`

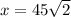
Q6.

Look at the first picture.

In a triangle 45° - 45° - 90°, all sides are in ratio 1 : 1 : √2.

In a triangle 30° - 60° - 90°, all sidea are in ratio 1 : √3 : 2.

Look at the second picture.

from the triangle 45° - 45° - 90°

`a\sqrt2=8` multiply both sides by √√2 (use √a · √a = a)

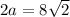`2a=8\sqrt2` divide both sides by 2

`a=4\sqrt2`

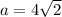
from the triangle 30° - 60° - 90°

`x=2a\to x=2(4\sqrt2)=8\sqrt2`

`y=a\sqrt3\to y=(4\sqrt2)(\sqrt3)=4\sqrt6`