Question

What is the thinnest soap film (excluding the case of zero thickness) that appears black when illuminated with light with a wavelength of 535 nm ? The index of refraction of the film is 1.33, and there is air on both sides of the film.

Answer 1

Step-by-step explanation:

It is given that,

The thinnest soap film appears black when illuminated with light with a wavelength of 535 nm,
`\lambda=5.35* 10^(-7)\ m`

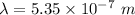
Refractive index,
`\mu=1.33`

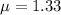
We need to find the thickness of soap film. The soap film appear black means there is an destructive interference. The condition for destructive interference is given by :

`2t=m(\lambda)/(\mu)`

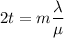
t = thickness of film

m = 0,1,2....

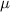`\mu` = refractive index

`t=m(\lambda)/(2\mu)`

`t=(\lambda)/(2\mu)`

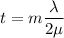
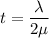
For thinnest thickness, m = 1

`t=1* (5.35* 10^(-7)\ m)/(2* 1.33)`

`t=2.01* 10^(-7)\ m`

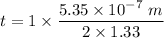
Hence, this is the required solution.