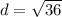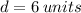ANSWER
The diagonal of the square is 6 units.
Step-by-step explanation
A diagonal of a square divides the square into two congruent right isosceles triangles.
Let the sides of the square be 's' units. Then, the Pythagoras Theorem says that, the sum of the squares of the shorter legs will be equal to the square of the hypotenuse.
Let the diagonal which is the hypotenuse be 'd' units.
Then,
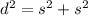
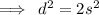
From the question, the side length of the square is
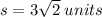
We plug in this value to obtain:
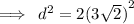
Or

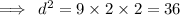
We take the positive square root of both sides to get: