Question

What is each power of i with its multiplicative inverse.

1. i

2. i ^2

3. i ^3

4. i ^4

Answer 1

1) multiplicative inverse of i = -i

2) Multiplicative inverse of i^2 = -1

3) Multiplicative inverse of i^3 = i

4) Multiplicative inverse of i^4 = 1

Explanation:

We have to find multiplicative inverse of each of the following.

1) i

The multiplicative inverse is 1/i

if i is in the denominator we find their conjugate

`=1/i * i/i\\=i/i^2\\=We\,\, know\,\, that\,\, i^2 = -1\\=i/(-1)\\= -i`

So, multiplicative inverse of i = -i

2) i^2

The multiplicative inverse is 1/i^2

We know that i^2 = -1

1/-1 = -1

so, Multiplicative inverse of i^2 = -1

3) i^3

The multiplicative inverse is 1/i^3

We know that i^2 = -1

and i^3 = i.i^2

`1/i^3\\=1/i.i^2 \\=1/i(-1)\\=-1/i * i/i\\=-i/i^2\\= -i/-1\\= i`

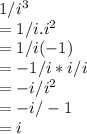
so, Multiplicative inverse of i^3 = i

4) i^4

The multiplicative inverse is 1/i^4

We know that i^2 = -1

and i^4 = i^2.i^2

`=1/i^2.i^2\\=1/(-1)(-1)\\=1/1\\=1`

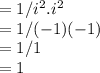
so, Multiplicative inverse of i^4 = 1