Question

The problem refers to triangle ABC. Find the area of the triangle. Round to three significant digits. B = 9° 20', C = 80° 40', b = 2.92 ft

Answer 1

Area of the triangle is 25.9 feet²

Explanation:

* Lets explain how to solve the problem

- In Δ ABC

∵ m∠ B = 9° 20' = 9 + 20/60 = (28/3)°

∵ b = 2.92 feet

- b is the side opposite to angle B

∵ m∠ C = 80° 40' = 80 + 40/60 = (242/3)°

- Lets find c the side opposite to angle C by sing the sine rule

∵
`(b)/(sinB)=(c)/(sinC)`

∴
`(2.92)/(sin(28/3))=(c)/(sin(242/3))`

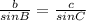
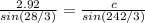
- By using cross multiplication

∴
`c=(2.92(sin(242/3))/(sin(28/3))=17.77`

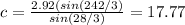
- The area of the triangle = 1/2 (b)(c)sin∠A

∵ The sum of the interior angles of a triangle is 180°

∴ m∠ A + m∠ B + m∠ C = 180°

∵ m∠ B = (28/3)°

∵ m∠ C = (242/3)°

∴ m∠ A + 28/3 + 242/3 = 180

∴ m∠ A + 90° = 180° ⇒ subtract 90 from both sides

∴ m∠ A = 90°

∴ Area of the triangle = 1/2 (2.92)(17.77) sin(90)

∵ sin(90) = 1

∴ Area of the triangle = 1/2 (2.92)(17.77) = 25.9 feet²

* Area of the triangle is 25.9 feet²