Answer:
The correct answer is H.
Explanation:
In order to solve this exercise we have two paths. The first one uses less calculation than the second.
First way of solution: Isolate the variable
in the right hand side of each equation. To do this you only need to divide the first equation by 2, and then divide the second equation by 3. Thus, you will obtain
and
.
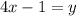Now, notice that both lines have the same slope, so they are parallel. But before to give a definite answer we need to check if both lines are the same or not. Evaluate at
, in the first equation you have
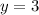and in the second one
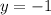. As they have different intercepts with the X-axis, they parallel.
Second way of solution: Solve the system of equations. Isolate
in the first equation:
.
Then, substitute this expression in the second equation:
.
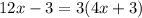
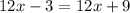Which is equivalent to
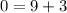and this is impossible. Hence, the system of equations has no solution and the lines are parallel.