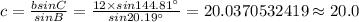Question

In △ABC, m∠A=15°, a=9, and b=12. Find c to the nearest tenth.

Answer 1

20.0 unit ( approx )

Explanation:

Here,

ABC is a triangle in which,

m∠A=15°, a=9, and b=12,

By the law of sine,

`(sin A)/(a)=(sin B)/(b)=(sin C)/(c)----(1)`

`(sin A)/(a)=(sin B)/(b)`

`\implies sin B=(b sin A)/(a)`

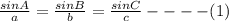
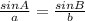
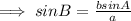
By substituting the values,

`\implies sin B=(12* sin 15^(\circ))/(9)\approx 0.3451`

`\implies B \approx 20.19^(\circ)`

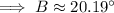
Now, by the property of triangle,

m∠A + m∠B+ m∠C = 180°

⇒ m∠C = 180° - 15° - 20.19° = 144.81°,

By the equation (1),

`c=(b sin C)/(sin B)=(12* sin 144.81^(\circ))/(sin 20.19^(\circ))=20.0370532419\approx 20.0`

Answer 2

=20.0

Explanation:

We can first find the angle B using the sine rule as follows:

a/Sin A=b/Sin B

9/Sin 15=12/ Sin B

Sin B= (12 Sin 15)/9

=0.345

B=Sin⁻¹ 0.345

=20.18°

We then find C by using the summation of the interior angles of a triangle.

C=180-(20.18+15)

=144.82

Finding the length of c:

a/Sin A= c/ Sin C

9/Sin 15=c/Sin 144.82

c=(9 Sin 144.82)Sin 15

=20.0