Question

Find an equation for the line perpendicular to y=−15x+3 with x-intercept at x = 3.

Write your answer in the form y=mx+b

Answer 1

bearing in mind that perpendicular lines have negative reciprocal slopes, let's find the slope of the provided line then

`\bf y=\stackrel{\stackrel{m}{\downarrow }}{-15}x+3\qquad \impliedby \begin{array}ll \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{-15\implies -\cfrac{15}{1}}\qquad \qquad \qquad \stackrel{reciprocal}{-\cfrac{1}{15}}\qquad \stackrel{negative~reciprocal}{+\cfrac{1}{15}\implies \cfrac{1}{15}}}`

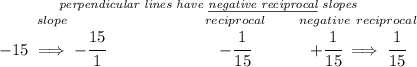
well, we know the x-intercept is at x = 3, recall when a graph intercepts the x-axis y = 0, so this point is (3 , 0). Then we're really looking for the equation of a line whose slope is 1/5 and runs through (3 , 0).

`\bf (\stackrel{x_1}{3}~,~\stackrel{y_1}{0})~\hspace{10em} slope = m\implies \cfrac{1}{5} \\\\\\ \begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-0=\cfrac{1}{5}(x-3)\implies y=\cfrac{1}{5}x-\cfrac{3}{5}`