Question

A projectile is fired vertically with an initial velocity of 192 m/s. Calculate the maximum altitude h reached by the projectile and the time t after firing for it to return to the ground. Neglect air resistance and take the gravitational acceleration to be constant at 9.81 m/s2.

Answers:

h = m
t = s

Answer 1

a) Maximum height reached = 1878.90 m

b) Time of flight = 39.14 seconds.

Step-by-step explanation:

Projectile motion has two types of motion Horizontal and Vertical motion.

Vertical motion:

We have equation of motion, v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration and t is the time taken.

Considering upward vertical motion of projectile.

In this case, Initial velocity = vertical component of velocity = u sin θ, acceleration = acceleration due to gravity = -g
`m/s^2` and final velocity = 0 m/s.

0 = u sin θ - gt

t = u sin θ/g

Total time for vertical motion is two times time taken for upward vertical motion of projectile.

So total travel time of projectile ,
`t=(2usin\theta )/(g)`

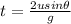
Vertical motion (Maximum height reached, H) :

We have equation of motion,
`v^2=u^2+2as`, where u is the initial velocity, v is the final velocity, s is the displacement and a is the acceleration.

Initial velocity = vertical component of velocity = u sin θ, acceleration = -g, final velocity = 0 m/s at maximum height H

`0^2=(usin\theta) ^2-2gH\\ \\ H=(u^2sin^2\theta)/(2g)`

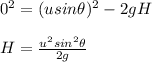
In the give problem we have u = 192 m/s, θ = 90° we need to find H and t.

a)
`H=(u^2sin^2\theta)/(2g)=(192^2* sin^290)/(2* 9.81)=1878.90m`

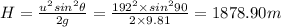
Maximum height reached = 1878.90 m

b)
`t=(2usin\theta )/(g)=(2* 192* sin90)/(9.81)=39.14s`

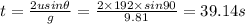
Time of flight = 39.14 seconds.