Answer:
The correct answer is: Option: C
C. 0<a<1
Explanation:
We are given a graph of a exponential function as:
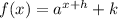
We know that the function is a exponential decay function if: 0<a<1
and it represents a exponential growth function if: a>1
Hence, by looking at the graph we observe that the graph is continuously decreasing with increasing values of x.
This means that the graph is a graph of exponential decay function.
Hence, we get: 0<a<1