Answer:
The correct option is B.
Explanation:
Given information: In ΔEDF, FE=20 m and height = 10 m. In ΔADC, AC=125 m.
From the given information, we conclude that AC║EF.
In ΔEDF and ΔADC,
 (Alternate interior angles)
(Alternate interior angles)
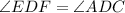 (Vertically opposite angle)
(Vertically opposite angle)
By AA rule of similarity,

The corresponding sides of two similar triangles are similar. So in ΔEDF and ΔADC,

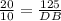
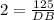
On cross multiplication, we get
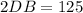
Divide both sides by 2.
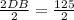
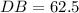
Therefore the correct option is B.