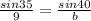Answer:
B.
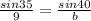
Explanation:
We are given that in a triangle ABC.
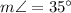
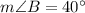
a=9
We have to find an equation which solve for b
We know that a sine law
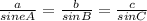
Using above formula of sine law
Substituting all given values in the above formula of sine law
Then we get
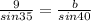
By cross multiply then we get
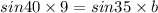
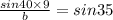
Using division property of equality
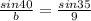
Using division property of equality
Hence, option B is true option for solving b.
Answer:B.