Answer:
f(-2) = 5/9
Explanation:
* lets explain the problem
∵ f(x) = 5(3)^x
- It is an exponential function
- (3) is the base of the function
- x is the exponent
- To find f(-2) means substitute x by -2
∵
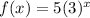
∵ x = -2
∴
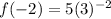
- If the power of the base is negative we can change its sign to
positive by reciprocal the base
# Ex:
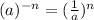
- Lets do that withe the base 3 and power -2
∵
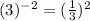
∴
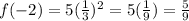
* f(-2) = 5/9