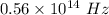Answer:
The equilibrium vibrational frequency that causes the shift is
Step-by-step explanation:
Given that,
Wavelength of Raman line
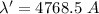
Wavelength
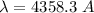
We need to calculate the frequency
Using formula of frequency
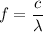
For 4748.5 A
The frequency is
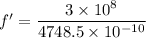
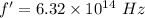
For 4358.3 A
The frequency is
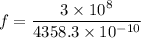

We need to calculate the shift
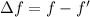
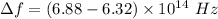
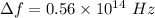
Hence, The equilibrium vibrational frequency that causes the shift is